会议时间：2021年12月4日-6日（周六-周一）
线上地址：腾讯会议 852 3393 4327
组织者：刘彦麟 熊金钢 许孝精 薛留堂
资助：“双一流”团队项目
|
2021年12月4日
|
|
时间
|
题目
|
报告人
|
地点
|
|
8:30-9:25
|
Uniform Bound of the Highest-order Energy of the 2D Incompressible Elastodynamics
|
蔡圆
复旦大学
|
腾讯会议：
85233934327
|
|
9:30-10:25
|
Zero-viscosity limit of the Navier-Stokes equations in a thin domain
|
王渝西
四川大学
|
|
午 休
|
|
14:00-14:55
|
The well-posedness of axially symmetric compressible subsonic jet impinging flow
|
程建峰
四川大学
|
腾讯会议：
85233934327
|
|
15:00-15:55
|
Some recent works about incompressible and compressible MHD equations
|
朱异
华东理工大学
|
|
2021年12月5日
|
|
时间
|
题目
|
报告人
|
地点
|
|
14:00-14:55
|
Liner Stability of Pipe Posieuille Flow at High Reynolds Number Regime
|
陈琦
中科院华罗庚中心
|
后主楼1220
腾讯会议：85233934327
|
|
15:00-15:55
|
The Optimal Decay Rate of Strong Solution for the Compressible Navier-Stokes Equations and related models with Large Initial Data
|
魏正珍
北京理论物理与计算数学研究所
|
|
16:00-16:55
|
From conservative to dissipative systems through quadratic change of time
|
段祥龙
首都师范大学
|
|
2021年12月6日
|
|
时间
|
题目
|
报告人
|
地点
|
|
14:00-14:55
|
Remarks on well-posedness of the generalized SQG equation
|
于幻
北京信息科技大学
|
腾讯会议：85233934327
|
|
15:00-15:55
|
Leray's flow-past-obstacle problem: uniqueness and the invading domains method
|
任潇
复旦大学
|
报告题目和摘要
Uniform Bound of the Highest-order Energy of the 2D Incompressible Elastodynamics
蔡圆
复旦大学
Abstract: This talk concerns the time growth of the highest-order energy of the systems of two dimensional incompressible isotropic Hookean elastodynamics. This two dimensional systems are nonlocal quasilinear wave equations where the unknowns has slow temporal decay. By observing an inherent strong null structure, the global well-posedness of smooth solutions near equilibrium was first proved by Zhen Lei where the highest-order generalized energy may have certain growth in time. We improve the result and show that the highest-order generalized energy is uniformly bounded for all the time.
The well-posedness of axially symmetric compressible subsonic jet impinging flow
程建峰
四川大学
Abstract： This talk is concerned with the well-posedness theory of the impact of a subsonic axially symmetric jet emerging from a semi-infinitely long nozzle, onto a rigid wall. The fluid motion is described by the steady isentropic Euler system. We showed that there exists a critical value M_{cr}>0, if the given mass flux is less than M_{cr}, there exists a unique smooth subsonic axially symmetric jet issuing from the given semi-infinitely long nozzle and hitting a given uneven wall. The surface of the axially symmetric impinging jet is a free boundary, which detaches from the edge of the nozzle smoothly. It is showed that a unique suitable choice of the pressure difference between the chamber and the atmosphere guarantees the continuous fit condition of the free boundary. Moreover, the asymptotic behaviors and the decay properties of the impinging jet and the free surface in downstream were also obtained. This is a joint work with Prof. Lili Du (SCU) and Prof. Qin Zhang (CQJTU).
Liner Stability of Pipe Posieuille Flow at High Reynolds Number Regime
陈琦
中科院数学与系统科学研究院
Abstract：In this paper, we prove the linear stability of the pipe Poiseuille flow for general perturbations at high Reynolds number regime. This is a long-standing problem since the experiments of Reynolds in 1883. Our work lays a foundation for the theoretical analysis of hydrodynamic stability of pipe flow, which is one of the oldest yet unsolved problems of fundamental fluid dynamics.
From conservative to dissipative systems through quadratic change of time
段祥龙
首都师范大学
Abstract：There are many examples of dissipative systems that can be derived from conservative ones. A classical example is the heat equation (or more generally the porous medium equation) that can be derived from the Euler equations of isentropic gases. The derivation can be done in many ways. In this talk, we will focus on a very straightforward idea: just perform the quadratic change to the time variable $\theta=t^2/2$.
Leray's flow-past-obstacle problem: uniqueness and the invading domains method
任潇
复旦大学
Abstract: We study the exterior problem for stationary Navier–Stokes equations in two dimensions describing a viscous incompressible fluid flowing past an obstacle. Two main results in the small Reynolds numbers regime will be presented: (i) uniqueness of the classical Finn-Smith solutions (ii) justification of Leray's invading domains method proposed in 1933. In the proofs, we combine and develop the ideas of Amick (Acta Math 1988), asymptotic analysis for the Oseen system, and novel blow-down arguments. Moreover, we show two basic estimates for general stationary Navier-Stokes solutions based on the above methods, and discuss their applications. The talk is based on joint works with Mikhail Korobkov and Julien Guillod.
Zero-viscosity limit of the Navier-Stokes equations in a thin domain
王渝西
四川大学
Abstract： In this talk, we justify the limit from the Navier-Stokes system in a thin domain to the Hydrostatic Navier-Stokes/ Prandtl system for the convex initial data with Gevrey 3/2 regularity in the x variable, which is the optimal Gevrey index, and Sobolev regularity in the y regularity.
The Optimal Decay Rate of Strong Solution for the Compressible Navier-Stokes Equations and related models with Large Initial Data
魏正珍
北京理论物理与计算数学研究所
Abstract：In this talk, we are concerned with the optimal decay rate for large solution to the three dimensional compressible Navier-Stokes(CNS) equations and related models. More precisely, we established the upper and lower bounds of decay rates for the global solution of CNS equations when the initial perturbation is large and belongs to L^1(R^3)\cap H^2(R^3). In addition, these lower bounds of decay rate coincide with the upper one.
Remarks on well-posedness of the generalized SQG equation
于幻
北京信息科技大学
Abstract：In this talk, we are concerned with the Cauchy problem of the generalized surface quasi-geostrophic (SQG) equation in which the velocity field is expressed as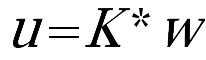 
, where 
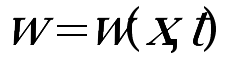is an unknown function and 
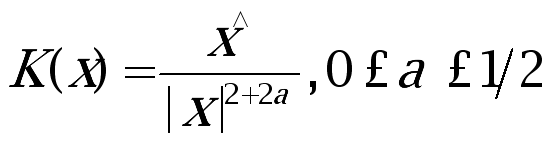. When
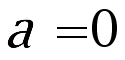, it is the two-dimensional Euler equations. When
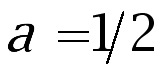, it corresponds to the inviscid SQG. We first present a new and elementary proof of the local existence and uniqueness of the classical solution via the method of the contraction mapping principle. Then, we prove stability of the (local) time of existence of smooth solutions with respect to 
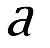. One implication is that the maximal time of existence
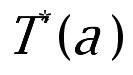, as a function of
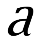, blows up as
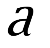approaches 0.
Some recent works about incompressible and compressible MHD equations
朱异
华东理工大学
Abstract: In this talk, we investigate the dissipative structure of both incompressible and compressible magnetohydrodynamic (MHD) systems. First, we focus on the 3D incompressible MHD equations with mixed partial dissipation and magnetic diffusion. Our main result assesses the global stability of perturbations near the steady solution given by a background magnetic field. Then we focus on the 2D compressible viscous and non-resistive MHD equations. We derive the global existence of small smooth solutions to this system on periodic domain.
