会议时间：2021年12月11日 星期六
腾讯会议 ID：538 405 621 会议密码：211211
邀请专家：
|
崔仁浩 （哈尔滨师大）
|
邓圣兵（西南大学）
|
|
耿俊（兰州大学）
|
罗海军（湖南大学）
|
|
罗森平（江西师范大学）
|
夏健康（西北工业大学）
|
|
杨敏波（浙江师范大学）
|
张建军（重庆交通大学）
|
组委会：唐仲伟 熊金钢 张程翔
资助：“双一流”团队项目、国家自然科学基金
会议日程
|
2021年12月11日 上午
|
|
时间
|
题目
|
报告人
|
主持人
|
|
8:30-8:40
|
开幕式
|
张程翔
|
|
8:30-9:10
|
Extrapolation, weighted Good-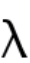 type bounds on Lipschitz domain, with application to Homogenization of Systems of Elasticity
|
耿俊
兰州大学
|
熊金钢
|
|
9:15-9:55
|
Concentration phenomenon of solutions for some fractional Yamabe type problems
|
邓圣兵
西南大学
|
|
10:10-10:50
|
A global branch approach to normalized solutions for Schrödinger equations
|
张建军
重庆交通大学
|
周路艳
|
|
10:55-11:35
|
On minima of sum of theta functions and application to Mueller-Ho Conjecture
|
罗森平
江西师范大学
|
|
2021年12月11日 下午
|
|
14:00-14:40
|
On critical Hartree equations: qualitative analysis and its applications
|
杨敏波
浙江师范大学
|
张程翔
|
|
14:45-15:25
|
Qualitative analysis on a reaction-diffusion-advection SIS epidemic
|
崔仁浩
哈尔滨师范大学
|
|
15:40-16:20
|
Saddle solutions for the critical Choquard equations
|
夏健康
西北工业大学
|
唐仲伟
|
|
16:25-17:05
|
Existence and stability of standing waves to the fractional Schrödinger equations with combined nonlinearities
|
罗海军
湖南大学
|
报告题目和摘要
Qualitative analysis on a reaction-diffusion-advection SIS epidemic model
崔仁浩
哈尔滨师范大学
Abstract： In this paper, we are concerned with a reaction-diffusion SIS epidemic model with standard incidence infection mechanism and linear source in advective heterogeneous environments. We have derived the threshold dynamics in terms of the basic reproduction number. We mainly investigate the effects of linear source, advection and diffusion on asymptotic profiles of the endemic equilibrium. It is shown that the linear source can enhance persistence of infectious disease, advection may cause the concentration phenomenon and small diffusion rate of infected individuals can eradicate the disease. These results may offer some implications on disease control and prediction.
Concentration phenomenon of solutions for some fractional Yamabe type problems
邓圣兵
西南大学
Abstract：In this talk, I will present some results about the existence and concentration phenomenon of solutions for some fractional Yamabe type problems. One is the existence of clustered solutions to low-order perturbations of fractional Yamabe equations, which are slightly supercritical, under certain geometric and dimensional assumptions, these solutions certainly exhibit non-isolated blow-up. The other is the instability of the fractional Yamabe problem under perturbations on the linear term, defined on the conformal infinity of an asymptotically hyperbolic manifold.
Extrapolation, weighted Good-
type bounds on Lipschitz domain, with application to Homogenization of Systems of Elasticity
耿俊
兰州大学
Abstract： For a family of systems of linear elasticity with rapidly oscillating periodic, bounded measurable coefficients, we give a sufficient condition for the weighted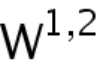 
estimates for weak solutions of Neumann problems in a fixed bounded Lipschitz domains by using a weighted real variable method.
Existence and stability of standing waves to the fractional Schrödinger equations with combined nonlinearities
罗海军
湖南大学
Abstract： We consider the fractional Schrödinger equations with combined nonlinearities and study the existence and stability of their solutions which have prescribed mass. More specifically, in the purely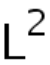 
-subcritical case, we show that the set of ground states is orbitally stable if the ground states exist. In the purely 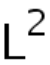-supercritical, we introduce two equivalent variational characterizations and use the profile decomposition of bounded sequences in 
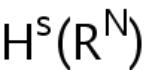to obtain the ground state solution. To prove the strong instability of its associated standing waves, we construct the third equivalent variational characterization and two invariant mainfolds to give the criterion of blow-up. Finally, in the combined-type cases, we prove the existence and strong instability of standing wave solutions, which is based on several equivalent variational characterizations and the virial estimate.
On minima of sum of theta functions and application to Mueller-Ho Conjecture
罗森平
江西师范大学
Abstract：Let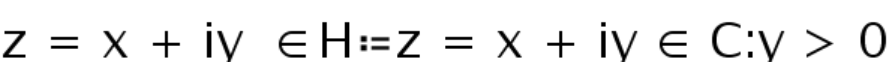 
and 
be the theta function associated with the lattice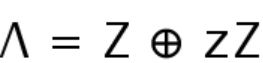 
. In this paper we consider the following pair of minimization problems
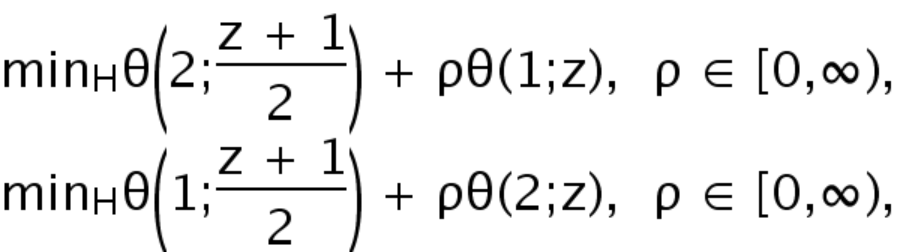
where the parameter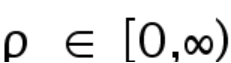 
represents the competition of two intertwining lattices, the particular selection of the parameters 
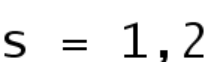is determined by the physical model, which can be generalized by our strategy and method proposed here. We find that as 
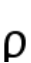varies the optimal lattices admit a novel pattern: they move from rectangular (the ratio of long and short sides changes from 
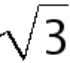to 1 continuously), square, rhombus (the angle changes from 
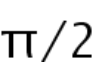to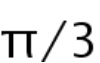 
continuously) to hexagonal continuously; geometrically, up to an invariant group(a subgroup of the classical modular group), they move continuously on a special curve; furthermore, there exists a closed interval of 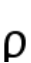such that the optimal lattices is always a square lattice. This is the first, novel and also the complete result on the minimizer problem for theta functions with parameter 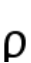. This is in sharp contrast to optimal lattice shapes for single theta function (
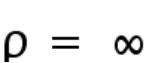case), for which the hexagonal lattice prevails. As a consequence, we give a partial and positive answer to optimal lattice arrangements of vortices in competing systems of Bose-Einstein condensates as conjectured (and numerically and experimentally verified) by Mueller-Ho.
Saddle solutions for the critical Choquard equations
夏健康
西北工业大学
Abstract：In this talk, I will present some results on the entirely nodal solutions for the critical Choquard equation. In a noncompact setting, by introducing suitable symmetric groups we constructed saddle solutions for the critical Choquard equation which illustrate the nonlocal feature of the Choquard equation and in contrast the local counterpart of the Yamabe equation has no such solutions. This is a joint work with Dr. Xu Zhang in Central South University.
On critical Hartree equations: qualitative analysis and its applications
杨敏波
浙江师范大学
Abstract：In this talk I will first introduce some qualitative properties of the solutions of the critical Hartree equation, such as the regularity, symmetry, decay estimates, classification and nondegeneracy. Then as an application of the properties, we will apply variational methods and Lyapunov-Schmidt reduction arguments to study the existence, multiplicity and blow-up phenomena of the nonlocal equation with Hardy-Littlewood-Sobolev critical exponents.
A global branch approach to normalized solutions for Schrödinger equations
张建军
重庆交通大学
Abstract：In this talk, we present a novel approach to study the existence, non-existence and multiplicity of prescribed mass positive solutions to a Schrodinger equation of the form
This approach permits to handle in a unified way nonlinearities which are either mass subcritical, mass critical or mass supercritical. Among its main ingredients is the study of the asymptotic behaviors of the positive solutions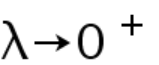 
or 
and the existence of an unbounded continuum of solutions in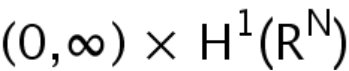 
. This is based on a joint work with Prof. Louis Jeanjean and Prof. Xuexiu Zhong
