
北京师范大学 非线性分析研讨会会议手册
为了促进非线性分析领域的交流与合作,我们将于2023年4月28日至5月2日在北京师范大学珠海校区(广东省珠海市)召开非线性分析研讨会。具体会议事宜如下:
一、 主办单位
北京师范大学
二、 会议时间
2023年4月28日至5月2日。4月28日报到,29、30日学术报告和交流,5月1日自由讨论,5月2日离会。
三、 会议地点
北京师范大学珠海校区国际交流中心二楼报告厅
四、 组织机构
学术委员会:保继光 曹道民 李岩岩 王志强
组织委员会:唐仲伟 熊金钢(18046512521) 张程翔(17611267897)
珠海联系人:张舒 (18811509406)
北京师范大学珠海分校国际交流中心:刘乐乐经理( 17788057119)
五、 会议资助
科技部重点研发项目、国家自然科学基金
六、 住宿地点
北京师范大学珠海校区国际交流中心、文华苑公寓
受邀专家
陈 化 武汉大学 |
邓引斌 华中师范大学 |
窦井波 陕西师范大学 |
桂长峰 澳门大学 |
郭玉霞 清华大学 |
黄荣里 广西师范大学 |
蒋美跃 北京大学 |
李东升 西安交通大学 |
李工宝 华中师范大学 |
李一梅 北京交通大学 |
刘自晓 北京工业大学 |
罗森平 江西师范大学 |
麻希南 中国科学技术大学 |
王 术 北京工业大学 |
王友德 中科院&广州大学 |
徐 露 湖南大学 |
严树森 华中师范大学 |
杨健夫 江西师范大学 |
杨孝平 南京大学 |
尹景学 华南师范大学 |
张志涛 中国科学院 |
周 风 华东师范大学 |
周蜀林 北京大学 |
邹文明 清华大学 |
会议日程
2023年4月29日上午 |
08:20—08:30 |
开幕式,主持人:熊金钢 |
|
报告人 |
主持人 |
08:30—09:10 |
尹景学 |
陈 化 |
09:20—10:00 |
徐 露 |
邹文明 |
10:00—10:20 |
茶歇、合影 |
10:20—11:00 |
张志涛 |
桂长峰 |
11:10—11:50 |
窦井波 |
杨孝平 |
2023年4月29日下午 |
14:00—14:40 |
严树森 |
蒋美跃 |
14:50—15:30 |
罗森平 |
郭玉霞 |
15:30—15:50 |
茶歇 |
15:50—16:30 |
李一梅 |
周 风 |
16:40—17:20 |
刘自晓 |
王 术 |
17:40—20:00 |
晚宴 |
2023年4月30日上午 |
08:30—09:10 |
麻希南 |
王友德 |
09:20—10:00 |
李东升 |
邓引斌 |
10:00—10:20 |
茶歇 |
10:20—11:00 |
周蜀林 |
杨健夫 |
11:10—11:50 |
黄荣里 |
李工宝 |
报告题目和摘要
Sharp weighted Sobolev inequality and affine weighted Sobolev inequality involving divergent operator on the upper half space
窦井波 陕西师范大学
Abstract: In this talk, we present a sharp weighted Sobolev inequality on the upper half space, which involves divergent operators with degeneracy on the boundary. All positive extremal functions are classified by the method of moving sphere and the uniqueness of ODE. As an application, based on analysis of the
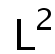
structure of gradient norm, we also establish some sharp affine weighted
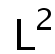
Sobolev inequalities on the upper half space involving a divergent operator.
On the second boundary value problem for special
Lagrangian curvature potential equation.
黄荣里 广西师范大学
Abstract: This is a sequel to (Huang and Ou in J Geom Anal 27:2601–2617, 2017) and (Chong et al. in On the second boundary value problem for Lagrangian mean curvature equation. Calc. Var. Partial Differential Equations 62 (2023), no. 3, Paper No. 74, 30 pp.), which study the second boundary problem for special Lagrangian curvature potential equation. As consequences, we obtain the existence and uniqueness of the smooth uniformly convex solution by the method of continuity through carrying out a-priori estimate on the solutions.
Pointwise interior Schauder estimates for Stokes
systems in divergence form
李东升 西安交通大学
Abstract: In this talk, we will first go over the history of Schauder estimates, where the developing of proofs will be emphasized. Second, we will establish pointwise interior Schauder estimates for Stokes systems in divergence form with variable coefficients. The estimates are presented by Campanato's characterization and are attained by an iteration method which was originated by L.Caffarelli to study Schauder estimates for fully nonlinear elliptic equations. Although no continuity in time variable is assumed for the coefficients and the given data, Holder continuity of curls of velocities is surprisingly obtained in both spatial variables and time variable.
Singular Yamabe type problems with an asymptotically flat metric
李一梅 北京交通大学
Abstract: In this talk, we study the asymptotic symmetry and local behavior of positive solutions at infinity to some conformal Laplacian equation defined on outside the bounded set in
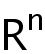
with asymptotically flat Riemannian metric g. We prove that the solution at infinity either converges to a fundamental solution of the Laplace operator on the Euclidean space or is asymptotically close to a Fowler-type solution defined on
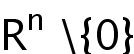
.
Existence of entire solutions to the Lagrangian mean curvature equations
刘自晓 北京工业大学
Abstract: We establish the existence and uniqueness theorem of entire solutions to the Lagrangian mean curvature equations with prescribed asymptotic behavior at infinity. The phase functions are assumed to be supercritical and converge to a constant in a certain rate at infinity. We develop new techniques to construct generalized symmetric super-solutions in entire space, which is very different from exterior Dirichlet problems.
The role of analysis in statistical physics: two models in 《PRL》and their solutions
罗森平 江西师范大学
Abstract: We show introduce two physical models in 《PRL》, including the Mueller-Ho model in 《PRL》(2002) and Messina-Löwen model in《PRL》(2003), and then present partial solutions to these two models. Two related questions will also be introduced and solutions will be given.
Liouville theorem for a class quasilinear elliptic equations in
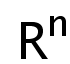
麻希南 中国科学技术大学
Abstract: We prove Liouville theorem for the equation
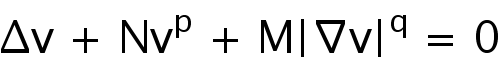
in
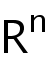
, with
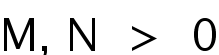
in the critical and subcritical case, in the radial case this was proved by Veron in Math Ann. 2020. In this talk we will delete the radial condition and get the same result. The proof is based on an integral identity. This is jointed work with Wu Wangzhe and Zhang Qiqi.
Some research on a class of
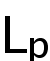
Minkowski type problem
徐 露 湖南大学
Abstract: In this talk, we will firstly introduce the
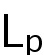
minkowski type problem for mixed k-Hessian operators. Then we will prove the existence and uniqueness of the admissible solutions when
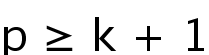
. Moreover, we can obtain the geometric convex solutions by using full rank theorem. At last, we will investigate the uniqueness of uniformly convex solutions when
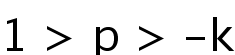
. This result implies that the self-similar solutions of the corresponding curvature flow converge to a round point.
Stable critical points for the Kirchhoff-Routh type functions
严树森 华中师范大学
Abstract: The study of blow-up solutions will lead to the investigation of the stable critical points of the Kirchhoff-Routh type functions. In this talk, I will present some results on this aspect, with emphasis on the effects of the small holes in the domain on the existence and stability of the critical points.
Propagation properties for finite diffusion equations with time delay
尹景学 华南师范大学
Abstract: This talk is to survey the recent progress on the study of finite diffusion equations with time delay. I will report how the finiteness of diffusion affects the shape of traveling waves such as smooth, sharp, semi-waves, and how the delay-time causes the traveling wave to be oscillating. This talk is based on recent research papers joint with Ming Mei, Shanming Ji, Tianyuan Xu.
Integrability, regularity and symmetry of positive
solutions for Wolff type integral systems
张志涛 中国科学院
Abstract: We are concerned with the optimal integrability, regularity and symmetry of integrable solutions for the Wolff type integral systems.
Firstly, we prove the optimal integrability and boundedness of solutions by constructing a nonlinear contracting operator and applying the regularity lifting lemma. Moreover, we exploit the general regularity lifting theorem to derive the Lipschitz continuity as
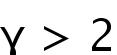
. We also prove that the solutions
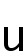
and
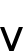
vanish at infinity. The results are valuable for the corresponding

-Laplace and
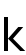
-Hessian systems.
Secondly, we use the method of moving planes to prove the symmetry and monotonicity of solutions as
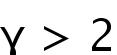
. Minkowski's inequality is crucial in our proofs. We believe that our arguments can be used to prove similar results for other Wolff type integral systems when
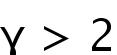
.
Well-posedness results on an oncolytic virotherapy model
周蜀林 北京大学
Abstract: I will talk about a haptotactic cross-diffusion system modeling oncolytic virotherapy accounting for interaction among normal cells and infected cancer cells, extracellular matrix and oncolytic viruses.